Cheol Hyeon

안녕하세요 :)

CNN(Convolution Neural Networks)

0. CNN이란?

CNN은 Convolution Neural Networks의 약자로 Convolution 기법이 쓰인 Neural Networks를 말한다.

한국어로는 합성곱 신경망 또는 그냥 컨벌루션 신경망 등으로 불린다.

그럼 여기서 말하는 convolution(합성곱)은 무엇일까?

합성곱이란 두 함수 중 하나를 반전(reverse), 이동(shift)한 뒤에 다른 하나의 함수와 곱해서 적분하여 새로운 함수를 구하는 것을 뜻한다.

수학 기호로 표시하면 다음과 같이 나타낼 수 있다.

Continuous convolution

\((f * g)(t)=\int f(\tau) g(t-\tau) d \tau\) 위 식을 합성곱의 정의대로 분석해보면

함수 $g(\tau)$ 를 반전 $g(-\tau)$ , 그리고 $t$만큼 이동시킨 후에 $g(-(\tau - t)) = g(t-\tau)$

함수 $f(\tau)$와 곱하여 $ f(\tau) g(t-\tau)$ 적분 $\int f(\tau) g(t-\tau) d \tau$ 한 것이다.

Discrete convolution

\[(f * g)(t)=\sum_{i=-\infty}^{\infty} f(i) g(t-i)\]

2D image convolution

\((I * K)(i, j)=\sum_m \sum_n I(m, n) K(i-m, j-n)\) 실제 CNN에서는 바로 위의 2D imgae convolution 의 식처럼 계산한다.

I가 이미지 데이터를 뜻하고 K는 우리가 이미지에 적용할 커널 또는 필터 뜻한다.

1. 등장 배경

CNN이 등장하기 전에는 일반적인 DNN(Deep Neural Networks)이 존재했다.

DNN 에서는 입력데이터를 1차원으로 평탄화(flatten)시켜 주어야했는데 문제점이 있었다.

이미지 데이터의 경우 보통 3차원의 구조를 갖는데 1차원으로 쭉 펴준다음에 사용해야만 하는 것이다.

여기서의 문제점은 데이터의 형상(shape)이 무시가 된다는 점이다.

데이터의 형상이 무시가 되면서 형상에 담겨있는 공간적인 정보가 사라지게 되는 것이다.

이미지를 예로 들면, 3차원의 데이터 공간에서 서로 가까운 픽셀값은 비슷한 정보를 담고 있을 수 있고 반대로 서로 멀리 떨어져 있는 픽셀값은 연관이 없는 등, 3차원에서만 가질 수 있는 공간적인 정보를 무시하게 된다.

하지만 CNN은 데이터를 그대로 받아들여 데이터 고유의 공간성을 이해함으로써 기존 Neural Networks의 단점을 개선 시킨 것이다.

2. 합성곱 연산

합성곱 연산의 과정은 아래와 같다.

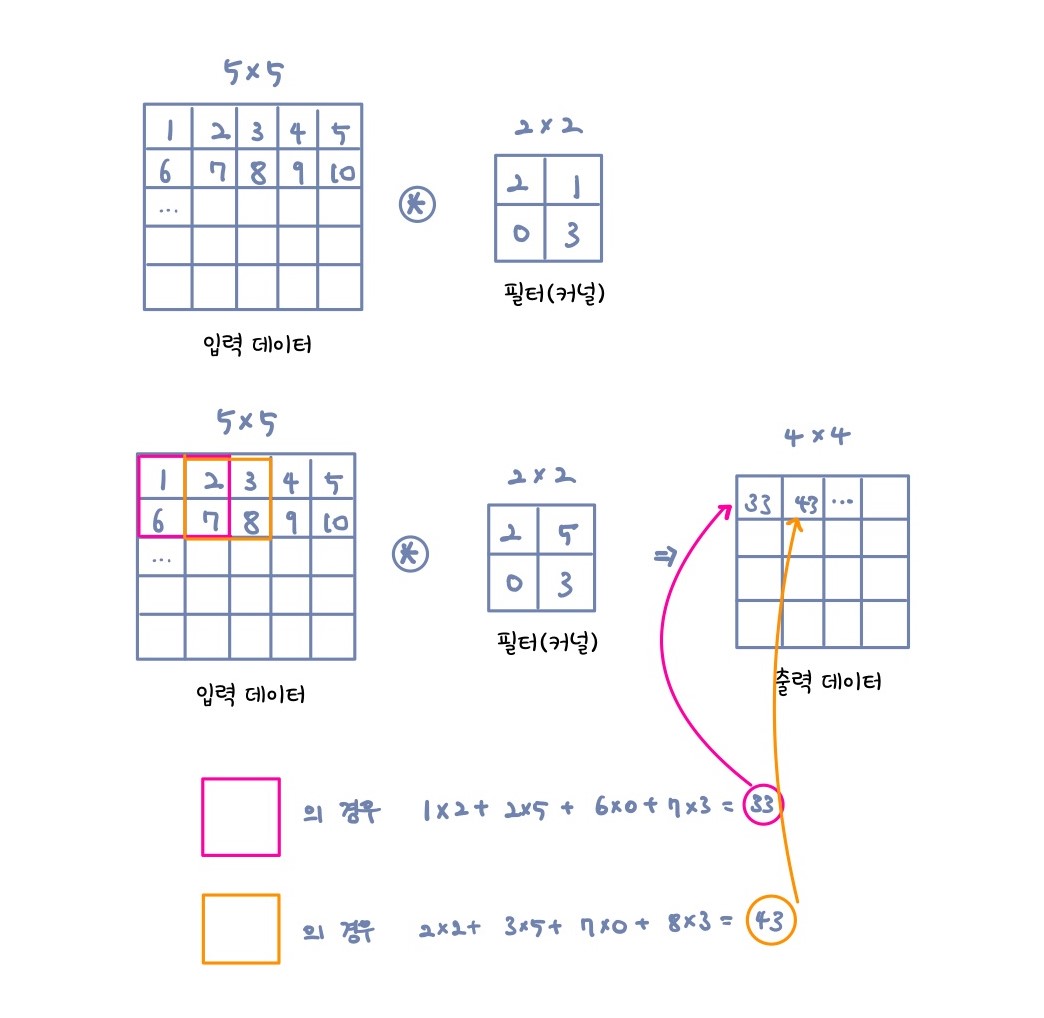
convolution_operation

입력 데이터에 필터(커널)을 적용 시킨다고 생각하면된다.(도장을 땅땅 찍듯이)

여기서 필터는 일반적인 신경망에서의 가중치 역할을 한다고 보면된다.

커널을 한칸씩 움직이면서 입력 데이터에 적용하여 element-wise하게 곱한 후 더해서 출력하는 방식이다.

$5\times5$ 입력 데이터를 $2\times2$ 필터를 적용시킬 경우 $4\times4$ 의 출력데이터가 나온다.

RGB Image의 경우 3개의 channel을 갖게되는데 예를 들어 $32\times32\times3$ 이미지에 $5\times5\times3$ 커널을 사용하게 되면 $28\times28\times1$ 출력데이터가 나오게 된다.

여기서 출력데이터는 특성맵(feature map)이라고 부르고 n개의 feature를 얻고싶으면 n개의 커널을 사용하면된다.

3. 패딩과 스트라이드

다음으로 알아볼 것이 패딩과 스트라이드 기법이다.

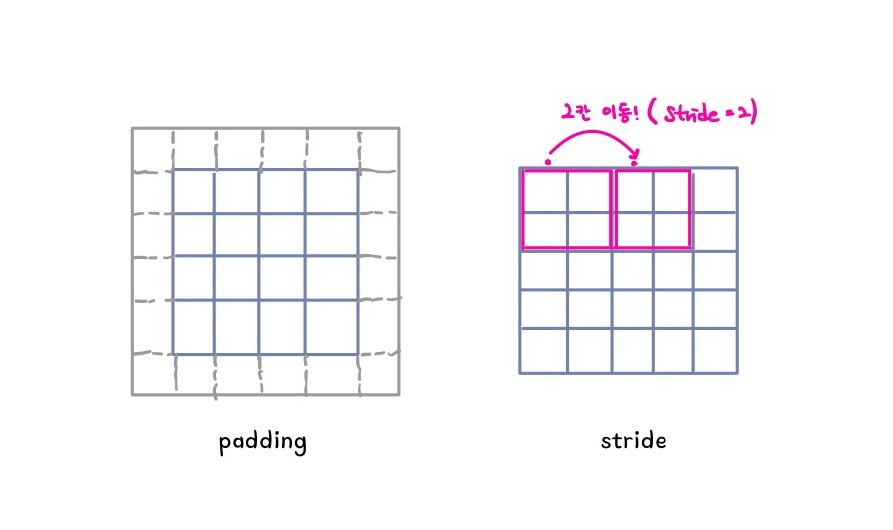
padding_stdie

위의 그림과 같이 패딩은 입력데이터 주변에 padding = 1을 추가하여 데이터 크기를 키워주는 것이다.

합성곱 연산을 여러번 하다보면 출력데이터의 크기가 점점 줄어드는데 패딩을 사용함으로써 출력 크기를 조정해줄 수 있다.

보통 zero-padding이라 하면 0으로 숫자들을 채우는 것을 말한다.

스트라이드의 경우 필터를 이동시킬 간격을 정해주는 역할을 한다.

위 그림에서는 stride = 2 인 경우인데 필터가 2칸 이동 한 것을 알 수 있다.

입력데이터의 크기, 커널의 크기, 패딩, 스트라이드가 주어졌을 때 출력데이터의 크기는 다음과 같이 구할 수 있다.

  • (H, W): 입력의 크기
  • (FH, FW): 필터의 크기
  • (OH, OW): 출력의 크기
  • P, S: 패딩, 스트라이드
\[OH=\frac{H+2P-FH}{S}+1 \\ OW=\frac{W+2P-FW}{S}+1\]

4. CNN을 구성하는 계층

  1. convolution layer
    • 커널을 적용시키는 곳
  2. Pooling layer
    • Max pooling(가장 높은 값만 추출)
    • Average pooling(평균 값을 추출)
  3. Fully connected layer
    • 최종적인 결과값을 만들어 주는곳

Convolution layer와 Pooling layer는 이미지에서 유용한 정보를 뽑아내는 곳

Fully connected layer에서는 최종적인 의사결정을 내려서 내가 원하는 정보를 얻어내는 곳

최근에는 Fully connected layer를 줄이는 추세이다. 왜냐하면 parameter 숫자를 줄여 학습을 좀더 쉽게 해주고 generalization performance를 향상 시키는 방향으로 가고있기 때문이다.

Fully connected layer의 parameter개수는 input의 크기와 output의 크기의 곱이기 때문에 convolution layer보다 훨씬 크다.

5. 파라미터수 계산

아래와 같은 정보가 주어졌을 때 해당 convolution layer를 정의하기 위한 파라미터의 숫자는 몇개일까?

  • input channel: 128
  • output channel: 62
  • kernel: $3\times3$

kernel에 channel이 명시되진 않았지만 자동적으로 input의 channel수와 동일하다.

따라서 $3\times3\times128$이 되고 output의 channel수만큼 있어야 하기때문에

최종적으로 $3\times3\times128\times64 = 73728$개 이다.

파라미터숫자는 패딩과 스트라이드의 영향을 받지 않으며 네트워크마다 갖고있는 parameter수가 대략 몇개 정도인지는 파악하고 있는 것이 중요하다.

6. $1\times1$ Convolution

  • Dimension reduction
    • 여기서 말하는 dimension은 channel 을 뜻한다.
    • 예를 들어 $256\times256\times128$ 데이터의 special dimension인 $256\times256$은 그대로 유지한 채 $1\times1\times128\times32$ 커널을 적용시켜 $256\times256\times32$ 결과를 만들어 내는 것
  • Convolution을 깊게 쌓으면서 parameter 수는 줄일 수 있는 효과

7. Networks

7.0 ILSVRC

  • ImageNet Large-Scale Visual Rrecognition Challenge

  • 2015년도에 ResNet이 Error Rate 3.5% 달성
  • 인간의 Error Rate가 대략 5.1%인걸 고려했을 때 엄청난 발전

7.1 Alexnet

  • 당시 부족한 GPU때문에 네트워크가 두개로 분리되어 있음(2개의 GPU사용)
  • $11\times11$, $5\times5$, $3\times3$ 3개의 filter를 사용
  • 5개의 convolution layers 와 3개의 dense layers로 구성
  • ReLU(Rectified Linear Unit) activation function을 사용
  • Data Augmentation
  • Dropout
  • number of parameters: 60M

현재는 위의 특징들이 당연시 여겨지지만 당시에는 획기적인 생각이였다고 한다.

ReLU Activation

  • $R(z) = max(0, z)$ 형태의 그래프를 가진 함수로 선형모델들의 특징들이 보존되어있음
  • 선형적인 특징때문에 gradient descent를 최적화하기 쉬움
  • vanishing gradient problem 문제를 극복해냈음
  • parameter를 initialize 할 때 He initialization을 사용

7.2 VGGNet

  • $3\times3$ convolution filter만을 사용
  • Dropout
  • layer 숫자에 따라 VGG16, VGG19로 나뉜다
  • number of parameters: 110M

왜 $3\times3$ 필터만들 사용했을까?

3by3

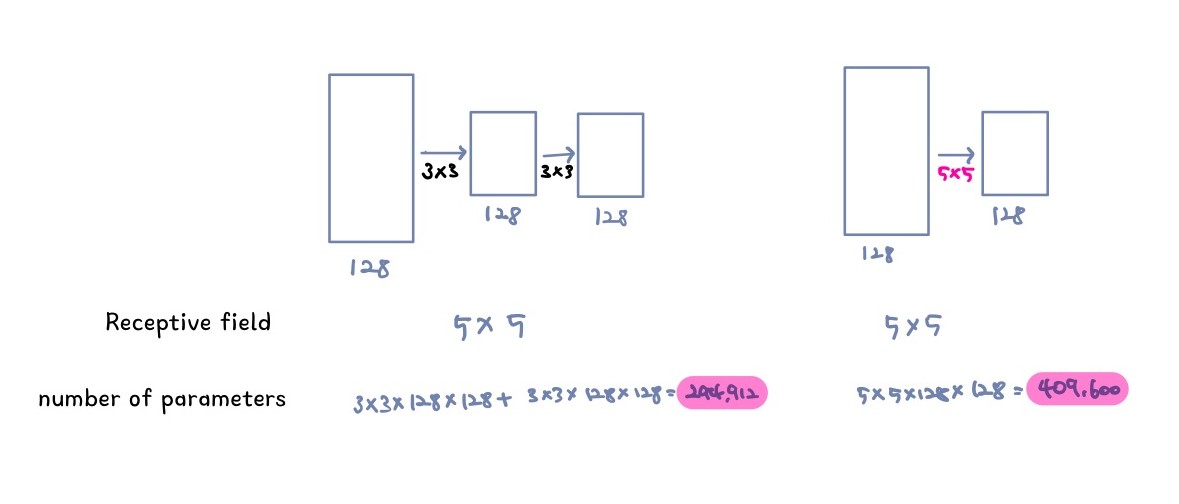
같은 Recpetive field를 얻지만 $3\times3$ filter의 경우 parameter수가 더 작음을 알 수 있다.

Receptive field 계산 $r_{i-1} = s_i\times r_i + (k_i - s_i)$

(k: kernel size, r: receptive field, s: stride)

7.3 GoogLeNet

  • 22 layers
  • 비슷한 모양의 네트워크가 전체 네트워크안에서 반복됨(network-in-network)
  • number of parameters: 4M
  • Inception Block

inception block

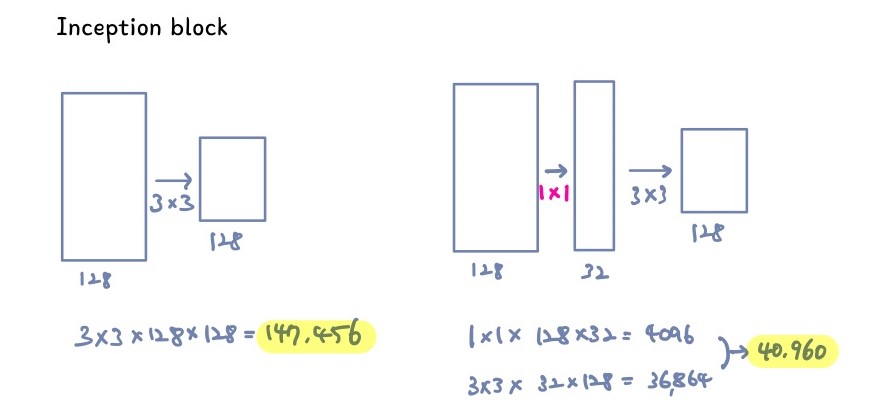
입력과 출력만 두고 봤을때는 똑같은데 파라미터 숫자가 현저히 줄어든 것을 볼 수 있다.

7.4 ResNet

network가 깊어질수록 파라미터 숫자가 많아짐에 따라 훈련을 하기 어렵다.

층이 깊어질 수록 좋은 성과를 내기를 기대했지만 오히려 더 안좋은 상황이 발생했다.

Identiy map이란 것을 사용해 극복!

  • Identity map
    • $f(x)$만 출력하는 것이 아닌 $f(x) + x$를 출력하도록 하는것
    • skip-connection 이라고도 한다
  • Batch Noramlization이 Convolution 다음에 나옴

7.5 DenseNet

ResNet에서는 x를 더해주었지만(Identity map) DenseNet에서는 concatenation을 해줌

층이 쌓일 수록 채널이 기하급수적으로 커지게된다.

  • Dense Block
    • 계속해서 concat 해주는 곳
  • Transition Block
    • Dense Block에서 늘어난 channel수를 줄여주는 곳

댓글남기기