Context-aware Recommendation
1. 개요
현재까지의 추천시스템들
- 유저와 아이템이 제공한 explicit 데이터를 활용, 또는 유저의 implicit 데이터 활용
- 주어진 데이터로부터 유저-아이템 행렬을 만든다
- 유저와 아이템 간의 관계, 유저와 아이템 특징을 활용
Matrix Factorization기법을 활용한 Collaborative Filtering의 한계
- 유저의 데모그래픽이나 아이템의 카테고리 및 태그 등 여러 특성(feature)들을 반영할 수 없음
- 상호작용 정보가 부족할 경우 cold start에 대한 대처가 어려움
유저, 아이템 등 직접적으로 관련된 정보이외의 다른걸 활용할 수는 없을까?!
Context - aware Recommender System
- Context: 맥락
- 맥락을 이해한다 = 유저의 상황을 이해한다
- 개체(유저 또는 아이템)의 상황을 설명하는 특징적인 정보를 뜻함
- Context-aware Recommender System = 맥락기반 추천시스템
- 맥락(유저의 상황)을 이해한 추천 시스템
- 유저와 아이템의 단순 상호관계 뿐만 아니라 상황 정보도 포함한 포괄적인 추천시스템
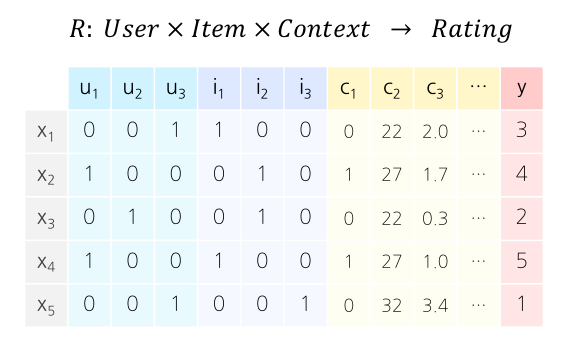
Model Structure
- 기존 방법
- Context-aware Recommender System
context 정보는 서비스에 따라 데이터 형태가 다르기때문에 feature들을 모두 담을 수 있는 general한 모델이 설계되어야 한다!
\[R:user\ \times \ item\ \times \ \color{red}{context} \color{black} \rightarrow rating\]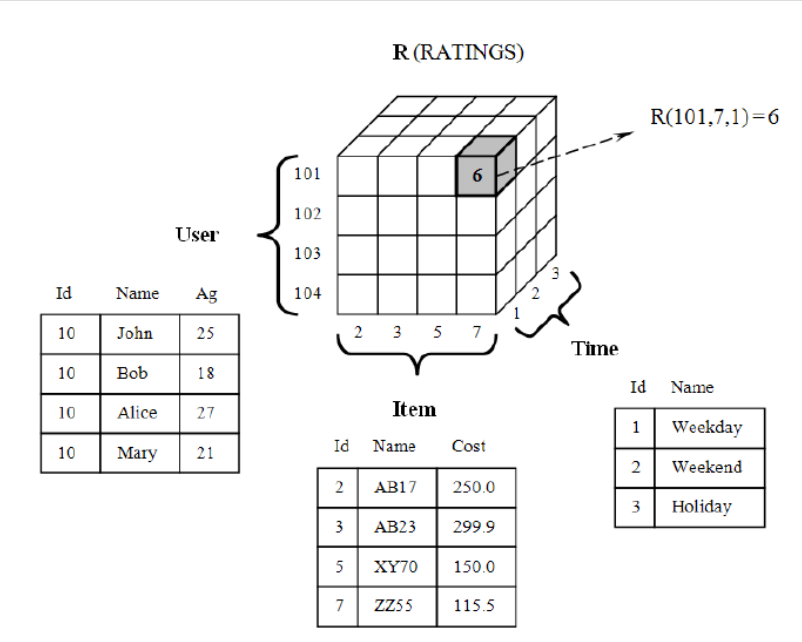
2. 특징
- 다양한 상황에서 주어지는 많은 context 정보 활용이 가능하다
- 주로 시간, 장소 등 정보가 활용된다
- 다양한 메타정보, 대표 키워드, 태그 등
- Context 정보를 얻는 방법도 다양하다
- Explicit하게 또는 Implicit하게 얻을 수 있음
- 접속한 기기, 날짜, 날씨 정보 등
- 적절한 context 정보로 초기 filtering을 할 수 있다
- Context 정보를 활용하여 A/B test 등 다양한 실험을 할 수 있다
- Context-Aware 추천시스템은 도메인 지식을 더욱 잘 활용할 수 있는 방법이다
| How Contextual Factors Change | Fully Obervable | Partially Observable | Unobservable |
|---|---|---|---|
| Static | Everything Known about Context | Partial and Static Context Knowledge | Latent Knowledge of Context |
| Dynamic | Context Relevance Is Dynamic | Partial and Dynamic Context Knowledge | Nothing Is Known about Context |
3. Methods
- Contextual Pre-filtering
- Context 정보를 활용하여 처음 데이터를 filtering 하는 기법
- Context 정보를 기준으로 user 또는 item을 나누는 방법
- Contextual Post-filtering
- User, item, contextual information 등 다양한 features로 모델링을 먼저 진행
- 모델의 추천결과에 context 정보를 활용하여 filtering하는 기법
- Contextual Modeling
- Context 정보 자체를 모델링에 활용하는 기법
- Complex한 방법으로 머신러닝 등의 모델을 활용할 수 있음
Contextual Pre-filtering
- Main Method
- Context 정보를 활용하여 가장 관련있는 2D (Users X Item) 데이터를 만든다
- 그 후에, 다양한 추천 알고리즘을 사용
- Context는 query의 역할로써 가장 관련있는 데이터를 선택하는 역할을 한다
- Context generalization
- $<girfriend, wine, friday>:$ too specific context
- Specific한 context 데이터가 충분하지 않기 때문에 sparsity 문제가 발생할 수 있다
- Context를 활용한 User-Item Split을 할 때, generalization을 할 필요가 있다
- 적절한 Filtering을 위해 computation이 많이 필요할 수 있다
Contextual Post-filtering
- Main Method
- Context 정보를 무시하고, User와 Item 정보로 2D 추천시스템 모델을 먼저 학습
- 추천 결과를 context 정보를 활용하여 filter 또는 adjust 한다
- 유저의 specific 취향 또는 패턴을 context를 통해 찾을 수 있다
- Heuristic approach
- 주어진 context로 특정 user가 관심있는 공통 item의 특징을 활용
- Model-based approach
- 주어진 context로 user가 item을 선호할 확률을 예측하는 모델을 만드는 방법
- Context generalization을 적용할 수 있으며 대부분의 잘 알려진 추천 알고리즘을 적용 가능
Contextual Modeling
- Main Method
- 모든 정보(user, item, context)를 전부 활용하여 모델링
- Predictive model 또는 Heuristic approach를 사용
- 기존 2D에서 N-Dimension 형태로 확장하여 모델링
- 예시
- Context-aware SVM
- Tensor Factorization, Pairwise Interaction Tensor Factorization
- Factorization Machine
4. Click-Through Rate Prediction
- CTR 예측: 유저가 주어진 아이템을 클릭할 확률을 예측하는 문제
- 추천시스템에서 online A/B test를 할때 가장 많이 쓰이는 지표 중 하나
- 예측해야 하는 y값은 클릭여부(0 또는 1)이므로 이진분류 문제에 해당
- 모델에서 출력한 값을 시그모이드 함수에 통과시켜 (0, 1) 사이의 예측 CTR 값을 얻어냄
- 광고에서 주로 사용
- 광고 클릭 횟수 = 돈!

- 광고가 노출된 상황의 다양한 유저, 광고, 컨텍스트 피쳐를 모델의 입력 변수로 사용
- 유저 ID가 존재하지 않는 데이터도 다른 유저 피쳐나 컨텍스트 피쳐를 사용하여 예측 가능
- 실제 현업에서는 유저 ID를 피쳐로 사용하지 않는 경우가 많다함
- 광고 클릭 횟수 = 돈!
이진 분류 문제 - 로지스틱 회귀(Logistic Regression
Basic model
\[logit(P(y=1|x))=(w_0+\sum_{i=1}^nw_ix_i), \ w_i\in R\]변수들간의 상호작용을 모델에 반영할 수 없음
Polynomial Model
\[logit(P(y=1|x))=(w_0+\sum_{i=1}^nw_ix_i +\sum_{i=1}^n\sum_{j=i+1}^nw_{ij}x_ix_j), \ w_i,w_{ij}\in R\]변수들간의 상호작용을 고려했을 때 파라미터 수가 급격하게 증가함(n의 k제곱으로 증가)
Dense Feature vs. Sparse Feature
- Dense Feature: 벡터로 표현했을 때 비교적 작은 공간에 밀집되어 분포하는 수치형 변수
- ex) 유저-아이템 평점, 기온, 시간 등
- Sparse Feature: 벡터로 표현했을 때 비교적 넓은 공간에 분포하는 범주형 변수
- one-hot encoding 또는 multi-hot encoding으로 표현
- ex) 요일, 분류, 키워드, 태그 등
CTR 예측 문제에 사용되는 데이터의 구성 요소는 대부분 Sparse Feature!
Feature Embedding
- One-hot Encoding 의 한계: 파라미터 수가 너무 많아질 수 있음
- 따라서 피쳐 임베딩을 한 이후에 이 피쳐를 가지고 예측을 함
- Item2Vec
- Latent Dirichlet Allocation(Topic Modeling)
- BERT(Pretrained Language Model)
5. Factorization Machines
SVM과 MF와 같은 Factorization Model의 장점을 결합
5.1 개요
Factorization Machine(FM)의 등장 배경
- 딥러닝이 등장하기 이전에는 SVM이 가장 많이 사용되는 모델이였음
- SVM: 커널 공간을 활용하여 비선형 데이터에 대해서 높은 성능을 보이는 모델
- 매우 Sparse한 데이터(CF환경)에 대해서는 SVM보다는 MF계열의 모델이 더 높은 성능을 보임!
- 하지만 MF모델은 특별한 환경, 즉 $X:(user,item)\rightarrow Y:(rating)$으로 이루어진 데이터에 대해서만 적용이 가능
SVM과 MF의 장점을 결합한 것은 없을까?!
5.2 FM 공식
\[\hat{y}(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^n \sum_{j=i+1}^n<v_i,v_j>x_ix_j \\ w_0,w_i \in R, \ v_i\in R^k\]- $w_0:$ Global Bias
- $\sum_{i=1}^nw_ix_i:$ modeling $ith \ weight$
- $\sum_{i=1}^n \sum_{j=i+1}^n<v_i,v_j>x_ix_j:$ Factorization term, Pairwise feature interaction
앞에 Polynomial Model과 비교했을 때 k 차원의 벡터를 factorization시켜 좀 더 일반화 시켰음!
5.3 FM 활용
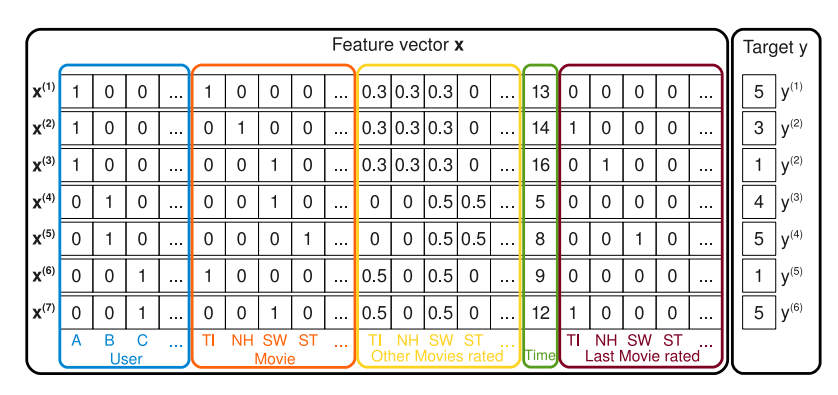
유저 A의 ST에 대한 평점 예측하기
- $v_A:$ 유저 B, C가 유저 A와 공유하는 SW의 평점 데이터를 통해 학습
- $v_{ST}:$ 유저 B, C의 ST에 대한 평점 데이터를 통해 학습
FM 장점
- vs. SVM
- 매우 sparse한 데이터에 대해서 높은 예측 성능을 보임
- 선형 복잡도 $O(kn)$를 가지므로 수십억개의 학습 데이터에 대해서도 빠르게 학습
- 모델의 학습에 필요한 파라미터 개수도 선형적으로 비례
- vs. Matrix Factorization
- 여러 예측 문제(회귀 / 분류 / 랭킹)에 모두 활용 가능한 범용적인 지도학습 모델(General Predictor)
- 유저, 아이템 ID 외에 다른 부가 정보들을 모델의 피쳐로 사용 가능
- 어떠한 실수값으로 된 피쳐 벡터에 대해서도 적용 가능
Factorization Machine Computation
\[\begin{aligned} & \sum_{i=1}^n \sum_{j=i+1}^n\left\langle\mathbf{v}_i, \mathbf{v}_j\right\rangle x_i x_j\\ &= \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n\left\langle\mathbf{v}_i, \mathbf{v}_j\right\rangle x_i x_j-\frac{1}{2} \sum_{i=1}^n\left\langle\mathbf{v}_i, \mathbf{v}_i\right\rangle x_i x_i \\ &= \frac{1}{2}\left(\sum_{i=1}^n \sum_{j=1}^n \sum_{f=1}^k v_{i, f} v_{j, f} x_i x_j-\sum_{i=1}^n \sum_{f=1}^k v_{i, f} v_{i, f} x_i x_i\right) \\ &= \frac{1}{2} \sum_{f=1}^k\left(\left(\sum_{i=1}^n v_{i, f} x_i\right)\left(\sum_{j=1}^n v_{j, f} x_j\right)-\sum_{i=1}^n v_{i, f}^2 x_i^2\right) \\ &= \frac{1}{2} \sum_{f=1}^k\left(\left(\sum_{i=1}^n v_{i, f} x_i\right)^n-\sum_{i=1}^2 v_{i, f}^2 x_i^2\right) \end{aligned}\]맨 위에 식 $O(kn^2)$에서 마지막 줄 $O(kn)$로 표현 가능
FM 주요 keyword 3가지
- Sparse data
- Linear Complexity
- General Predictor
6. Field-aware Factorization Machines
6.1 개요
- Field-aware Factorization Machine(FFM)은 FM을 발전시킨 모델로서 PITF 모델에서 아이디어를 얻음
- PITF: Pairwise Interaction Tensor Factorization(MF를 확장시킨 모델)
- PITF에서는 $(user,item,tag)$ 3개의 필드에 대한 CTR을 예측하기 위해 $(user,item),(item,tag),(user,tag)$ 각각에 대해서 서로 다른 latent factor를 정의하여 구함
PITF의 아이디어를 일반화하여 여러개의 필드에 대해서 latent factor를 정의한 것이 FFM
FFM의 특징
- 입력 변수를 필드로 나누어 필드별로 서로 다른 latent factor를 가지도록 factorize함
- 기존의 FM은 하나의 변수 $x$에 대해서 k개로 factorize했으나 FFM은 f개의 필드에 대해 각각 k개로 factorize함
- Field는 모델을 설계할 때 함께 정의되며, 같은 의미를 갖는 변수들의 집합으로 설정
- 유저: 성별, 디바이스, 운영체제
- 아이템: 광고, 카테고리
- 컨텍스트: 어플리케이션, 배너
CTR예측에 사용되는 피쳐는 이보다 훨씬 다양한데, 피쳐의 개수만큼 필드를 정의하여 사용할 수 있음!
6.2 FFM 공식
\[\hat{y}(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^n \sum_{j=i+1}^n<v_{i,f_j},v_{j,f_i}>x_ix_j \\ w_0,w_i \in R, \ v_{i,f}\in R^k\]곱해지는 상대의 필드를 고려하여 factorization
FM / FFM 성능 비교
데이터의 표현방식에 따라 FM, FFM 성능이 다름!
어떤 데이터셋은 필드를 사용하지 않는 것이 더 적합할 수도 있음
따라서 이러한 데이터셋에 FFM을 적용하면 Overfitting / Underfitting의 가능성 존재
7. Gradient Boosting Machine (GBM)
7.1 개요
Gradient Boosting Machine을 통한 CTR 예측
CTR 예측을 통해 개인화된 추천 시스템을 만들 수 있는 또 다른 대표적인 모델
- 8개의 오픈 CTR 데이터 셋에 대해 다른 추천 모델(FM 계열 포함)보다 높은 성능을 보임
- 하쿠나 라이브 @ 하이퍼커넥트
- 서비스 데이터가 축적됨에 따라 초기의 인기도 기반 혹은 휴리스틱 기반 추천 시스템에서 탈피
- 실시간 서비스의 경우 다양한 환경에 따라 데이터의 특징이 자주 변하기 때문에 하이퍼파라미터에 비교적 민감하지 않은 robust 모델을 사용하고 싶어함
- (FM, FFM, Deep FM 모델) < (기존 사용하던 휴리스틱 모델) < (GBM 계열 모델)
7.2 GBM
Boosting
- 앙상블(Ensemble) 기법의 일종
- 모델의 편향에 따른 예측 오차를 줄이기 위해 여러 모델을 결합하여 사용하는 기법
- 의사결정 나무(decision tree)로 된 weak learner들을 연속적으로 학습하여 결합하는 방식
- weak learner: 정확도와 복잡도가 낮은 간단한 분류기
- 연속적: 이전 단계의 weak learner가 취약했던 부분을 위주로 데이터를 샘플링하거나 가중치를 부여해 다음 단계의 learner를 학습한다는 의미
- Boosting 기반 모델
- AdaBoost (Adaptive Boosting)
- Gradient Boosting Machine (GBM)
- XGBoost, LightGBM, CatBoost
Gradient Boosting
gradient descent를 사용하여 loss function이 줄어드는 방향(negative gradient)으로 weak learner들을 반복적으로 결합함으로써 성능을 향상시키는 Boosting 알고리즘
- 파라미터가 아닌 학습 learner 자체로 미분을 수행
- 이전 단계의 weak learner까지의 residual을 계산하여, 이를 예측하는 다음 weak learner를 학습함(통계학적 관점)
- 회귀 문제에서는 예측 값으로 residual을 그대로 사용하고 분류 문제에서는 log(odds) 값을 사용
- 손실 함수 값이 일정 수준 이하로 떨어지거나 leaf node에 속하는 데이터의 수가 적어지면 멈춤
장점
- 대체로 Bagging을 사용하는 random forest보다 나은 성능을 보임
단점
- 느린 학습속도(순차적으로 weak learner를 학습하기 때문)
- 과적합 문제(prediction shift)
- 모델이 계속해서 residual에 맞게 학습하기 때문
Gradient Boosting의 문제점을 해결하기 위한 대표적인 모델/라이브러리
- XGBoost
- Extreme gradient boosting의 약자로, 병렬처리 및 근사 알고리즘을 통해 학습 속도를 개선한 라이브러리
- LightGBM
- Microsoft에서 제안한, 병렬 처리 없이도 빠르게 Gradient Boosting을 학습할 수 있도록 하는 라이브러리
- CatBoost
- 범주형 변수에 효과적인 알고리즘 등을 구현하여 학습 속도를 개선하고 과적합을 방지하고자 한 라이브러리

댓글남기기